asked 2014-10-19 19:19:12 +0100
Ahoj,
snažím se zjistit, jestli je možné dokázat nějakou nerovnost tímto způsobem:
Mám zadanou nerovnost:
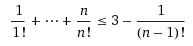pro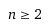 
Nejdřív vyzkouším n=2 -> platí Pak udělám n+1. Použiji indukční předpoklad, tam kde se dá a po úpravách mi vyjde
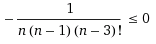
Což platí. Dá se toto považovat za důkaz, nebo ne? Pokud ne, jak by to šlo? :)
Díky za odpověď.
answered 2014-10-19 21:50:07 +0100
https://www.dropbox.com/s/4kkg2z2wzi0g4x9/IMG_20141019_214700.jpg?dl=0 Tady je postup, snad je to pochopitelný. Upravuješ tu sumu, až ti vyjde něco, co je menší než pravá strana v indukčním kroku, tím je to dokázaný.
Jinak sorry za papír, ale k přečtení to snad je, navíc nevím, jak tu psát rovnice. (+je to rychlejší :) )
answered 2014-10-19 20:46:22 +0100
Rekl bych, ze ano (pokud predpoklad byl pouzit). Navic se da to pekne prepsat na:
(2-n)/n!<=0; 2-n<=0 pro V n >=2;
Asked: 2014-10-19 19:19:12 +0100
Seen: 478 times
Last updated: Oct 19 '14
Copyright students of FIT CTU and others, 2014. Content on this site is licensed under a Creative Commons Attribution-ShareAlike 4.0 International license.
Indukcí to samozřejmě jde. Nerovnost je tvrzení jako každé jiné. Z popisu ale není jasné jak ten indukční předpoklad použijete a ten výraz co uvádíte se mi nezdá. Ofocená odpověď níže se zdá OK.
Tomáš Kalvoda ( 2014-10-19 23:02:24 +0100 )editUž jsem tam našel chybu. Moje blbost, jako vždy :) Díky
Trillian ( 2014-10-19 23:44:06 +0100 )edit