Revision history [back]
Důkaz nerovnosti matematickou indukcí
Ahoj,
snažím se zjistit, jestli je možné dokázat nějakou nerovnost tímto způsobem:
Mám zadanou nerovnost:
1/1! + ... n/n! <= 3 - 1/(n-1)! pro n >= 2
Nejdřív vyzkouším n=2 -> platí Pak udělám n+1. Použiji indukční předpoklad, tam kde se dá a po úpravách mi vyjde
-1/(n(n-1)(n-3)!) <= 0
Což platí. Dá se toto považovat za důkaz, nebo ne? Pokud ne, jak by to šlo? :)
Díky za odpověď.
Vložil bych obrázek, ale karma... :)
 | 2 | No.2 Revision |
Důkaz nerovnosti matematickou indukcí
Ahoj,
snažím se zjistit, jestli je možné dokázat nějakou nerovnost tímto způsobem:
Mám zadanou nerovnost:
1/1! + ... n/n! <= 3 - 1/(n-1)! 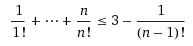 pro
pro n >= 2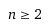
Nejdřív vyzkouším n=2 -> platí Pak udělám n+1. Použiji indukční předpoklad, tam kde se dá a po úpravách mi vyjde
-1/(n(n-1)(n-3)!) <= 0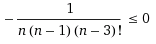
Což platí. Dá se toto považovat za důkaz, nebo ne? Pokud ne, jak by to šlo? :)
Díky za odpověď.
Vložil bych obrázek, ale karma... :)
 | 3 | retagged |
Důkaz nerovnosti matematickou indukcí
Ahoj,
snažím se zjistit, jestli je možné dokázat nějakou nerovnost tímto způsobem:
Mám zadanou nerovnost:
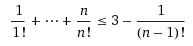 pro
pro 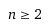
Nejdřív vyzkouším n=2 -> platí Pak udělám n+1. Použiji indukční předpoklad, tam kde se dá a po úpravách mi vyjde
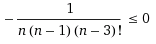
Což platí. Dá se toto považovat za důkaz, nebo ne? Pokud ne, jak by to šlo? :)
Díky za odpověď.
