Derivace lokální extrém

asked Dec 5 '14

V E-learningu jsem zaškrtl, že toto tvrzení je pravdivé :

"Pokud je derivace funkce f v bodě a nulová a f je spojitá, pak má f v a lokální extrém."

E-learningový test to vyhodnotil jako chybu, tak se ptám, proč ?

Pod tím bylo správné řešení toto: "Pokud je derivace funkce f v bodě a nulová nebo neexistuje, pak má f v a lokální extrém." Jelikož lze zaškrtávat více odpovědí jako správné, tak se ptám, proč je správně pouze tato varianta ?

Přikládám obrázek, pokud by to bylo z popisu nejasné.

Comments

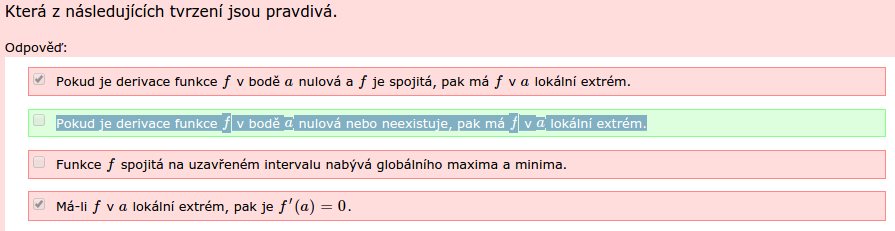
Není to náhodou tak, že druhá odpověď je zelená, protože je správně neoznačená? Tím pádem je špatně, že není zaškrtnutá třetí odpověď a ta je ta správná?

hansk (Dec 5 '14)

Je to tak, ty barvy jsou fakt matoucí.

shejby (Dec 6 '14)

add a comment

2

answered Dec 5 '14

Tomáš Kalvoda
960 ●10 ●16 ●24

Jak již bylo řečeno nulovost první derivace neimplikuje existenci extrému v daném bodě. Protipříkladem zmiňovaným i na přednášce je $x^3$ .

Dále je podstatné si uvědomit, co znamenají barvy v opravených odpovědích na eduxu. Zelená znamená, že jste nabízenou odpověď správně ne/zaškrtli. Tj. pokud to byla pravda, tak jste ji zaškrtli a pokud to byla nepravda, tak jste ji nezaškrtli. Červená barva označuje špatné zaškrtnutí. Jinak řečeno, barva neoznačuje pravdivost daných výroků, ale správnost vašeho zaškrtávání.

Není to můj nápad a nepřijde mi to jako nejvhodnější. Už se na to nachytala řada vašich kolegů.

link

Comments

Víc než to, že jsem to měl/neměl špatně mě právě rozhodily ty barvy.

shejby (Dec 6 '14)

To je pochopitelné :-).

Tomáš Kalvoda (Dec 6 '14)

Haha tomuhle se musim zasmát, protože přesně takhle jsem se ptal loni, taky mě ty barvy zmátly :D

relickus (Dec 6 '14)

add a comment

1

answered Dec 5 '14

Josef Kokeš
2956 ●20 ●35 ●73

updated Dec 5 '14

Protože nulová (nebo neexistující) derivace není postačující podmínka, ale nutná podmínka. Jednoduchý protipříklad je

$f(x) = x^3, f'(x) = 3x^2$ V bodě 0 je derivace 0, ale lokální extrém tam rozhodně není.

Z toho vyplývá, že ani to řešení označené jako správné ve skutečnosti správné není. Správně by mohlo být tvrzení číslo 3, pokud to "nabývá globálního maxima a minima" vztahujeme k tomu intervalu (nikoliv nutně k definičnímu oboru).

Ještě doplním další protipříklady:

$f(x) = x^3, x = 0$
$f(x) = \frac{1}{x}, x = 0$
$f(x) = x^3, x \in [-1, 1]$
$f(x) = \frac{1}{x^2}, x = 0$

link

Comments

Aha, možná jsem tu variantu 3 chápal jinak, než byla myšlena: Třeba tím autoři e-learningu chtěli říct, že ta funkce je spojitá na celém definičním oboru, a v takovém případě že nabývá na nějakém uzavřeném intervalu (který je podmnožinou definičního oboru) minima i maxima. To je pravda.

Já jsem původně to tvrzení chápal tak, že funkce je spojitá na uzavřeném intervalu, z čehož by mělo vyplývat, že někde na definičním oboru nabývá globálního minima a maxima - to pravda není.

Josef Kokeš (Dec 5 '14)

add a comment

Derivace lokální extrém

Comments

2 Answers

Comments

Comments

Your answer

Question tools

Stats

Related questions