Rešení kongruence
Prosim pomoc. Jak obecne, co nejefektivneji vyřesim nasledujici kongruenci.
(2^k)*x≡b (mod m)
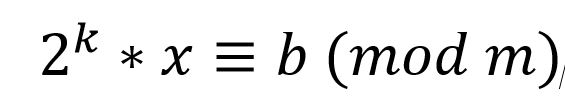 Děkuji
Děkuji
k, b a mod m znám
Prosim pomoc. Jak obecne, co nejefektivneji vyřesim nasledujici kongruenci.
(2^k)*x≡b (mod m)
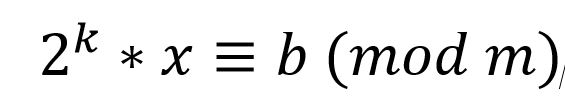 Děkuji
Děkuji
k, b a mod m znám
Jak nás učí MI-MPI: Rovnice má řešení pouze pokud je m liché (přesněji nesoudělné s 2^k), nebo pokud je b dělitelné největším společným dělitelem m a 2^k.
V prvním kroku bych nahradil 2^k číslem 2^k (mod m). Pak bych postupoval tak, jak je popsáno zde na slajdech 15 až 18. Jak funguje rozšířený Euklidův algoritmus najdete také v odkazovaných materiálech nebo také třeba zde.
Asked: 2016-11-01 17:46:09 +0100
Seen: 154 times
Last updated: Nov 17
 Copyright students of FIT CTU and others, 2014. Content on this site is licensed under a Creative Commons Attribution-ShareAlike 4.0 International license.
Copyright students of FIT CTU and others, 2014. Content on this site is licensed under a Creative Commons Attribution-ShareAlike 4.0 International license.
Rád Vám odpovím, ale musíte mi trochu ujasnit, co jsou ty písmenka. Je to tak, že m, b a k znáte a x je neznámá?
Karel Klouda ( 2016-11-03 09:22:45 +0100 )editDobrý den. Ano, k, b, a mod m znám. Hledám X. Prý to jde Euklidovým algoritmem ale prý to jde ještě rychleji jiným postupem. Omlouvám se za pozdní odpověd.
RadekS ( 2016-11-13 17:10:20 +0100 )edit