Algoritmus O(n^4)
asked 2015-03-17 02:38:09 +0100
Anonymous
Ahojte, muze mi nekdo prosim strucne vysvetlit ten algoritmus na FindByCost?
asked 2015-03-17 02:38:09 +0100
Anonymous
Ahojte, muze mi nekdo prosim strucne vysvetlit ten algoritmus na FindByCost?
EDIT2 Nejprve je to potřeba předpočítat tak, že si pro každý obdelník spočítáš součet plochy vlevo nad ním.
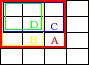
A = C+B-D
A pak si projdeš všechny obdélníky tím způsobem, že si každý obdélník spočítáš takto:
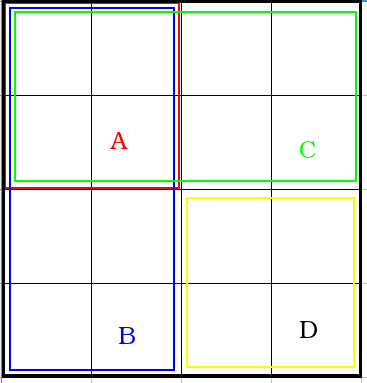
žlutá plocha = D - C - B + A
EDIT Níže uvedené řešení není O(n^4)
generuješ obdélníky délky 1x1 až NxN
pak je posouváš do všech míst kam to jde
a pro každé posunutí sečteš prvky uvnitř obdélníku.
A ty hledáš největší obdélník, který má ten součet menší nebo roven maxCost
Predpočítavaš si niečo, či len to "na sprosťáka" prejdeš?
PeterBocan ( 2015-03-17 22:54:44 +0100 )editza b) :D myslíš, že to nebude n^4? Sekvenčním testem mi to prošlo..
Ondřej Máca ( 2015-03-18 00:47:08 +0100 )editNo ja sa len pýtam, pretože to je n^4 a urobiť sumu z podmatice je n^2 tak nejako mi to nejde do hlavy, rozmýšľal som na Summed Area Table, ale obávam sa, že by to bolo zase "too much".
PeterBocan ( 2015-03-18 00:50:10 +0100 )editdneska jsem se na cvičení dozvěděl, že to skutečně n^4 není. Je na to prý potřeba algoritmus z PA1
Ondřej Máca ( 2015-03-18 20:42:13 +0100 )editTak závisí, čo tým mysleli, že to v skutočnosti nie je n^4.
PeterBocan ( 2015-03-18 22:59:08 +0100 )editno zkrátka, dělal jsem to tím nejnajivnějším algoritmem jakým to snad jde a o něm říkali, že má složitost myslím n^6. Ukazovali tam neco jako, ze si budes pamatovat sumu v levo nahore nad danym bodem. Ale do detailu to nevim. Ale nasel jsem dobrej navod na findByCrime http://kam.mff.cuni.cz/~kuba/ka/jak_zrychlovat.pdf část 1.5 Spokojil jsem se s tím řešením n^3 a i tak mám ve speedtestu mnohem lepší časy než ref. Asi to bude tim, ze je to sice O(n^3) ale pokud budou matice nahodne, tak bude prumerna slozitost n^2
Ondřej Máca ( 2015-03-19 00:23:19 +0100 )editAsked: 2015-03-17 02:38:09 +0100
Seen: 250 times
Last updated: Mar 20 '15
 Copyright students of FIT CTU and others, 2014. Content on this site is licensed under a Creative Commons Attribution-ShareAlike 4.0 International license.
Copyright students of FIT CTU and others, 2014. Content on this site is licensed under a Creative Commons Attribution-ShareAlike 4.0 International license.